When can machines learn?
机器学习应用的三个条件:
- 事物本身存在某种潜在规律
- 某些问题难以使用普通编程解决
- 有大量的数据样本可供使用
流程
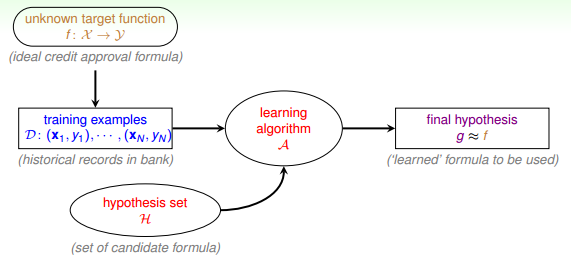
术语:
- 输入x
- 输出y
- 目标函数f,即最接近实际样本分布的规律
- 训练样本data
- 假设hypothesis,一个机器学习模型对应了很多不同的hypothesis,通过演算法A,选择一个最佳的hypothesis对应的函数称为矩g,g能最好地表示事物的内在规律,也是我们最终想要得到的模型表达式。
感知机(Perceptron)
$$ h(x) = sign ((\sum_{i=1}^n w_i x_i) - threshold)$$
其中 h(x) = 1/ -1, w是权重,threshold是阙值
把$threshold = w_0x_0 (x_0 =1)$,得到
$$ h(x) = sign ((\sum_{i=1}^n w_i x_i) - w_0x_0) $$
$$ = sign(\sum_{i=0}^n w_i x_i)$$
$$ = sign(W^TX) $$
假设只有二维,那么$ h(x) = w_0 + w_1x_1 + w_2x_2$,其中$w_0 + w_1x_1 + w_2x_2=0$是其中一条分类直线,权重w不同,代表不同的直线。
线性感知机 Perceptron Learning Algorithm(PLA)
- 逐步修正:首先在平面上随意取一条直线,看看哪些点分类错误。然后开始对第一个错误点就行修正,即变换直线的位置,使这个错误点变成分类正确的点。接着,再对第二个、第三个等所有的错误分类点就行直线纠正,直到所有的点都完全分类正确了,就得到了最好的直线。
做法:首先随机选择一条直线进行分类。然后找到第一个分类错误的点,如果这个点表示正类,被误分为负类,即$w_t ^t x_n(t)<0$,那表示w和x夹角大于90度,其中w是直线的法向量(垂直于这条直线)(ps:直线方程式的系数代表该直线的法向量)。所以,x被误分在直线的下侧(相对于法向量,法向量的方向即为正类所在的一侧),修正的方法就是使w和x夹角小于90度。通常做法是$w←w+yx, y=1$,如图右上角所示,一次或多次更新后的w+yx与x夹角小于90度,能保证x位于直线的上侧,则对误分为负类的错误点完成了直线修正。


保证数据是线性可分:假设有这样一条直线,能够将正类和负类完全分开,令这时候的目标权重为$w_f$,对于每一个点,满足$y_n = sign(w_f^t x_n)$, 那么即每一个到这条直线的距离都大于0,即对于每一个点t,满足:
$$ y_{n(t)} w_n^f x_{n(t)} >= min y_{n} w_n^f x_{n} > 0 $$PLA会对每次错误的点进行修正,更新权重$w_{t+1}$的值,如果$w_{t+1}与w_f$越来越接近,数学运算上就是内积越大,那表示证明PLA是有学习效果
的。
推导:
$$ w_f^T w_{t+1} = w_f^T(w_t + y_nx_n^t) $$
$$ = w_f^Tw_t + w_f^Ty_nx_n^t $$
$$ > w_f^Tw_t + 0 $$
$$ > w_f^Tw_t $$为了证明内积的增长不是由于长度而是夹角,推导:
当有错误的点的时候,即$ y_{n(t)} w_n^f x_{n(t)} <= 0 $
那么
$$ ||w_{t+1}||^2 = || w_t + y_{n(t)}x_{n(t)}||^2 $$
$$ = || w_t||^2 + 2w_ty_{n(t)}x_{n(t)} + ||y_{n(t)}x_{n(t)}||^2 $$
$$ <= || w_t||^2 + 0 + ||y_{n(t)}x_{n(t)}||^2 (y_n = 1/-1)$$
$$ <= || w_t||^2 + ||maxx_{n(t)}||^2 $$
所以 $||w_{t+1}||^2$的增长量不会超过$||maxx_{n(t)}||^2$- 如果$w_0 = 0$, 经过T次修正后,得 $ w_f^T \over ||wf||$$ w_T \over ||w_T||$$ >= \sqrt{T}*constant$
推导:

因$\sqrt{T}⋅constant≤1$,也就是说,迭代次数T是有上界的。
口袋算法 Packet Algorithm
对于非线性可分的PLA,容忍有错误点,取错误点的个数最少时的权重w。
分类
1. 按输出y的分类
- 监督学习
- 非监督学习
- 半监督学习
- 增强学习(Reniforcement Learning): 我们给模型或系统一些输入,但是给不了我们希望的真实的输出y,根据模型的输出反馈,如果反馈结果良好,更接近真实输出,就给其正向激励,如果反馈结果不好,偏离真实输出,就给其反向激励。不断通过“反馈-修正”这种形式,一步一步让模型学习的更好。

2. 按Data分类
- Batch Learning: 一次性拿到整个Data,对其进行学习建模。
- Online: 在线学习模型,数据是实时更新的,根据数据一个个进来,同步更新我们的算法。
PLA算法。
增强学习。
- Active Learning: 让机器具备主动问问题的能力,例如手写数字识别,机器自己生成一个数字或者对它不确定的手写字主动提问。

3. 按输入X的类型
- concrete features:具体的特征。
- raw features:比如说手写数字识别中每个数字所在图片的mxn维像素值;比如语音信号的频谱。
- abstract features:比如某购物网站做购买预测时,提供给参赛者的是抽象加密过的资料编号或者ID。

Python实现PLA
1 | def new_PLA(mat): |
Python实现Pocket算法
1 | def pocket(mat, iter_num = 50): |