Why can machines learn?
No Free Lunch定理
No Free Lunch定理表明,没有一个学习算法可以在任何领域总是产生最准确的学习器。不管采用何种学习算法,至少存在一个目标函数,能够使得随机猜测算法是更好的算法。
NFL说明了无法保证一个机器学习算法在D以外的数据集上一定能分类或预测正确,除非加上一些假设条件。
机器学习中假设与目标函数相等的可能性
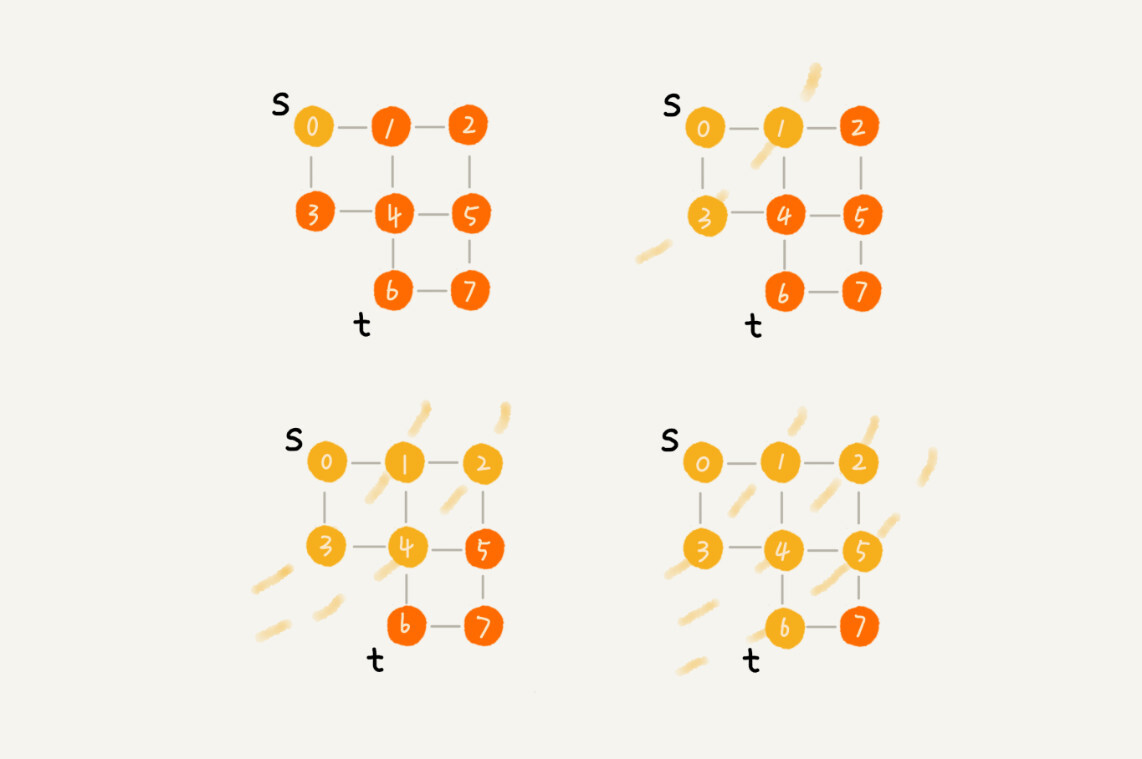
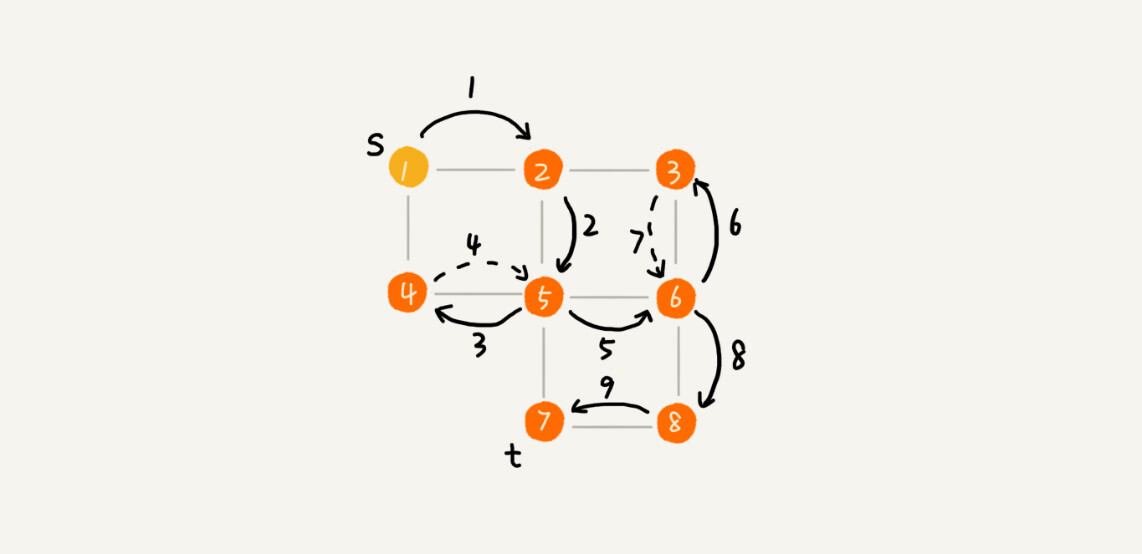
- 机器学习中hypothesis与目标函数相等的可能性,类比于罐子中橙色球的概率问题;罐子里的一颗颗弹珠类比于机器学习样本空间的x;橙色的弹珠类比于h(x)与f不相等;绿色的弹珠类比于h(x)与f相等;从罐子中抽取的N个球类比于机器学习的训练样本D,且这两种抽样的样本与总体样本之间都是独立同分布的。所以呢,如果样本N够大,且是独立同分布的,那么,从样本中h(x)!=f(x)的概率就能推导在抽样样本外的所有样本中h(x)!=f(x)的概率是多少。
- $E_{in}(h)$表示在抽样样本中,h(x)与$y_n$不相等的概率;$E_{out}(h)$表示实际所有样本中,h(x)与f(x)不相等的概率是多少。如果$E_{in}$很小,那么他们错误概率满足PAC,他们很接近。
- M是hypothesis的个数,N是样本D的数量,ϵ是参数。该union bound表明,当M有限,且N足够大的时候,Bad Data出现的概率就更低了,即能保证D对于所有的h都有$E_{in}~~E_{out}$,满足PAC,演算法A的选择不受限制。那么满足这种union bound的情况,我们就可以和之前一样,选取一个合理的演算法(PLA/pocket),选择使$E_{in}$最小的$h_m$作为矩g,一般能够保证$g≈f$,即有不错的泛化能力。
所以,如果hypothesis的个数M是有限的,N足够大,那么通过演算法A任意选择一个矩g,都有$E_{in}≈E_{out}$成立;同时,如果找到一个矩g,使
$E_{in}≈0$,PAC就能保证$E_{out}≈0$。至此,就证明了机器学习是可行的。

M对机器学习可行性的影响
- 从之前课程可以归纳出机器学习可行需要满足:
- $E_{in}(g)≈E_{out}(g)$
- $E_{in}(g)$ 足够小
- hypothesis set的个数M是有限的,但是当M很小时,不一定找到满足(2)的M,当M很大时,同样由霍夫丁不等式,$E_{in}(g)$与$E_{out}(g)$可能相差很大
- shatter : $m_H(H) = 2^N$ 即,exists N input can be shatter.也就是说对于inputs的所有情况都能列举出来。例如对N个输入,如果能够将$2^N$种情况都列出来,则称该N个输入能够被假设集H shatter。
- 二分类(dichotomy),dichotomy就是将空间中的点(例如二维平面)用一条直线分成正类(蓝色o)和负类(红色x),它的上界是$2^N$。
- 成长函数(growth function),记为$m_H(H)$,成长函数的定义是:对于由N个点组成的不同集合中,某集合对应的dichotomy最大,那么这个dichotomy值就$m_H(H)$,它的上界是$2^N$。
- break point,满足$m_H(H)=2^K$的k的最小值就是break point。那么令有k个点,如果k大于等于break point时,它的成长函数一定小于2的k次方。
- Vapnik-Chervonenkis(VC) bound

VC Dimension
- 假设空间H有break point k,那么它的成长函数是有界的,它的上界称为Bound function。根据数学归纳法,Bound function也是有界的,且上界为$N^{k-1}$

那么 vc bound可以转化为
这个式子的值只与k、N有关。 - VC Dimension:就是某假设集H能够shatter的最多inputs的个数,即最大完全正确的分类能力(注意,只要存在一种分布的inputs能够正确分类也满足)。根据之前break point的定义:假设集不能被shatter任何分布类型的inputs的最少个数。则VC Dimension等于break point的个数减一。即:
$$ d_{vc} = ‘min k’-1 $$ - $ d_{vc} = d+1$
- VC Dimension代表了假设空间的分类能力,即反映了H的自由度,产生dichotomy的数量,也就等于features的个数,但也不是绝对的。
- 将$d_{vc}$代表k,此时vc bound 为


ϵ表现了假设空间H的泛化能力,ϵ越小,泛化能力越大。
那么,可以得到
上述不等式的右边第二项称为模型复杂度,其模型复杂度与样本数量N、假设空间$H(d_{vc})$、ϵ有关。$E_{out}$由$E_{in}$共同决定。下面绘出$E_{out}$、model complexity、$E_{in}$随$d_{vc}$变化的关系:
- 样本复杂度(Sample Complexity),如果选定$d_{vc}$,样本D的数量N大约是$d_{vc}$的10000倍。这个数值太大了,实际中往往不需要这么多的样本数量,大概只需要$d_{vc}$的10倍就够了。
Noise and Error
错误衡量

错误衡量三个特性
- out-of-sample:样本外的未知数据
- pointwise:对每个数据点x进行测试
- classification:看prediction与target是否一致,classification error通常称为0/1 error
PointWise error实际上就是对数据集的每个点计算错误并计算平均

pointwise error一般可以分成两类:0/1 error和squared error。
- Ideal Mini-Target由P(y∣x)和err共同决定。
0/1 error中的mini-target是取P(y|x)最大的那个类,而squared error中的mini-target是取所有类的加权平方和。
Algorithmic Error Measure
- Error有两种:false accept和false reject。false accept意思是误把负类当成正类,false reject是误把正类当成负类。
- 机器学习演算法A的cost function error估计有多种方法,真实的err一般难以计算,常用的方法可以采用plausible或者friendly

Weighted Classification
机器学习的Cost Function即来自于这些error,也就是算法里面的迭代的目标函数,通过优化使得Error(Ein)不断变小。
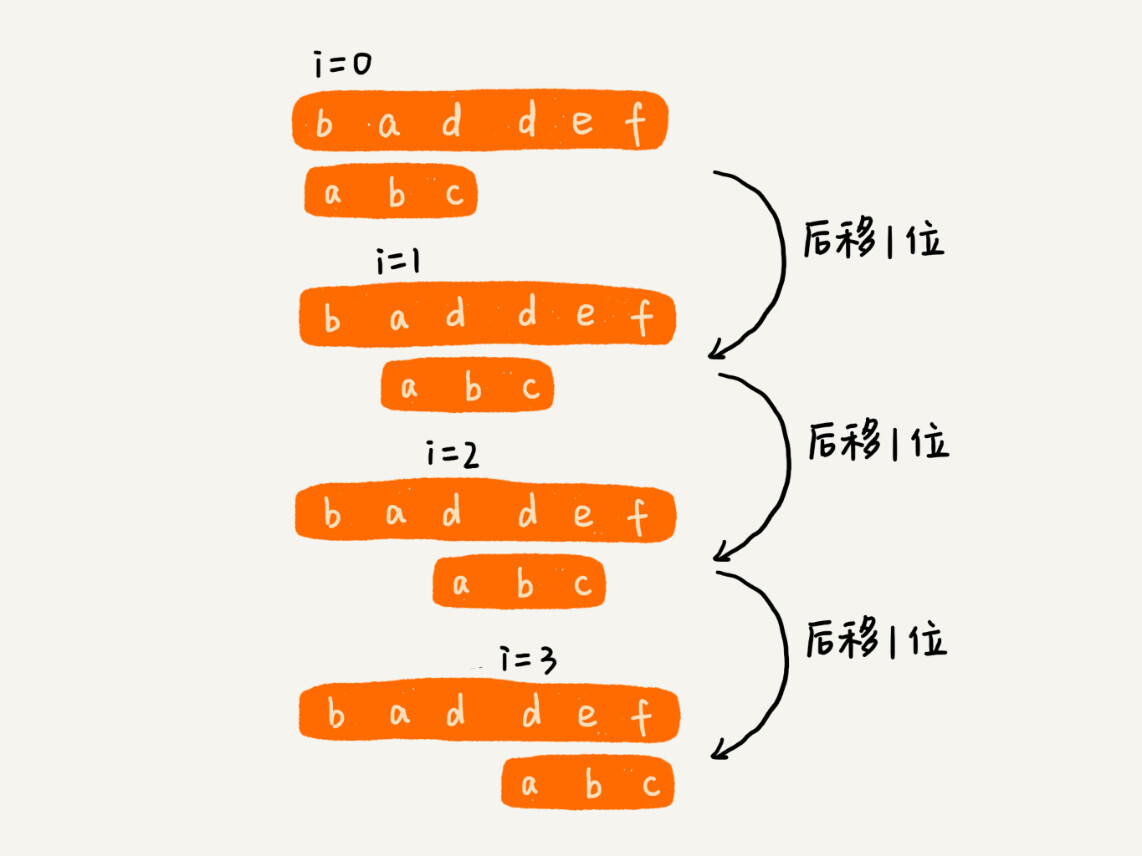
cost function中,false accept和false reject赋予不同的权重,在演算法中体现。对不同权重的错误惩罚,可以选用virtual copying的方法。